Analysis of equilibrium binding data obtained by linear-response spectroscopic techniques.
D Toptygin, L Brand
文献索引:Anal. Biochem. 224(1) , 330-8, (1995)
全文:HTML全文
摘要
A new computational approach for the analysis of equilibrium binding data obtained by spectroscopic methods is described. The approach is aimed at systems involving multiple interactions, where the changes in the spectroscopic signal cannot be attributed to a single interaction. A family of absorption or fluorescence spectra or decay curves obtained in a course of multiple titrations can be decomposed into basic components in an infinite variety of different ways. Model equilibrium equations are used as constraints to determine the basic components associated with the actual chemical species and the concentrations of these species. No assumption is made regarding the parametric form of the component spectra or decays. Binding constants are evaluated simultaneously with the resolved spectra and/or decays in a nonlinear least-square procedure. A key benefit of the method presented is the reduction in the number of fitting parameters. The conditions necessary and sufficient for the existence of a unique solution are considered. The application of the method is demonstrated with experimental data involving titrations of horse liver alcohol dehydrogenase with NADH and isobutyramide.
相关化合物
| 结构式 | 名称/CAS号 | 分子式 | 全部文献 |
|---|---|---|---|
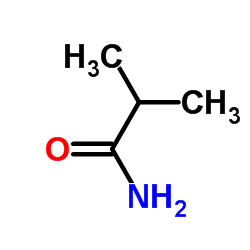 |
异丁酰胺
CAS:563-83-7 |
C4H9NO |
|
A New Signaling Pathway for HCV Inhibition by Estrogen: GPR3...
2016-01-01 [PLoS ONE 11 , e0145212, (2016)] |
|
Induction of fetal hemoglobin expression by the histone deac...
2003-03-01 [Blood 101(5) , 2001-7, (2003)] |
|
Effects of ketoacidosis on rat apolipoprotein A1 gene expres...
2000-08-01 [J. Mol. Endocrinol. 25(1) , 129-39, (2000)] |
|
Thermosensitive molecular assemblies from poly(amidoamine) d...
2011-07-04 [Angew. Chem. Int. Ed. Engl. 50(28) , 6332-6, (2011)] |
|
Oral isobutyramide reduces transfusion requirements in some ...
2000-11-15 [Blood 96(10) , 3357-63, (2000)] |